四探针原理｜薄膜电阻方程推导

为了确定如何使用四探针测量薄膜的薄层电阻，先假设一个简化的场景。想象一个任意尖锐的探针接触导电材料的半无限体积(除了朝向探针的方向外，其他方向都是无限的)，并将电流(通过施加的电压)注入其中。

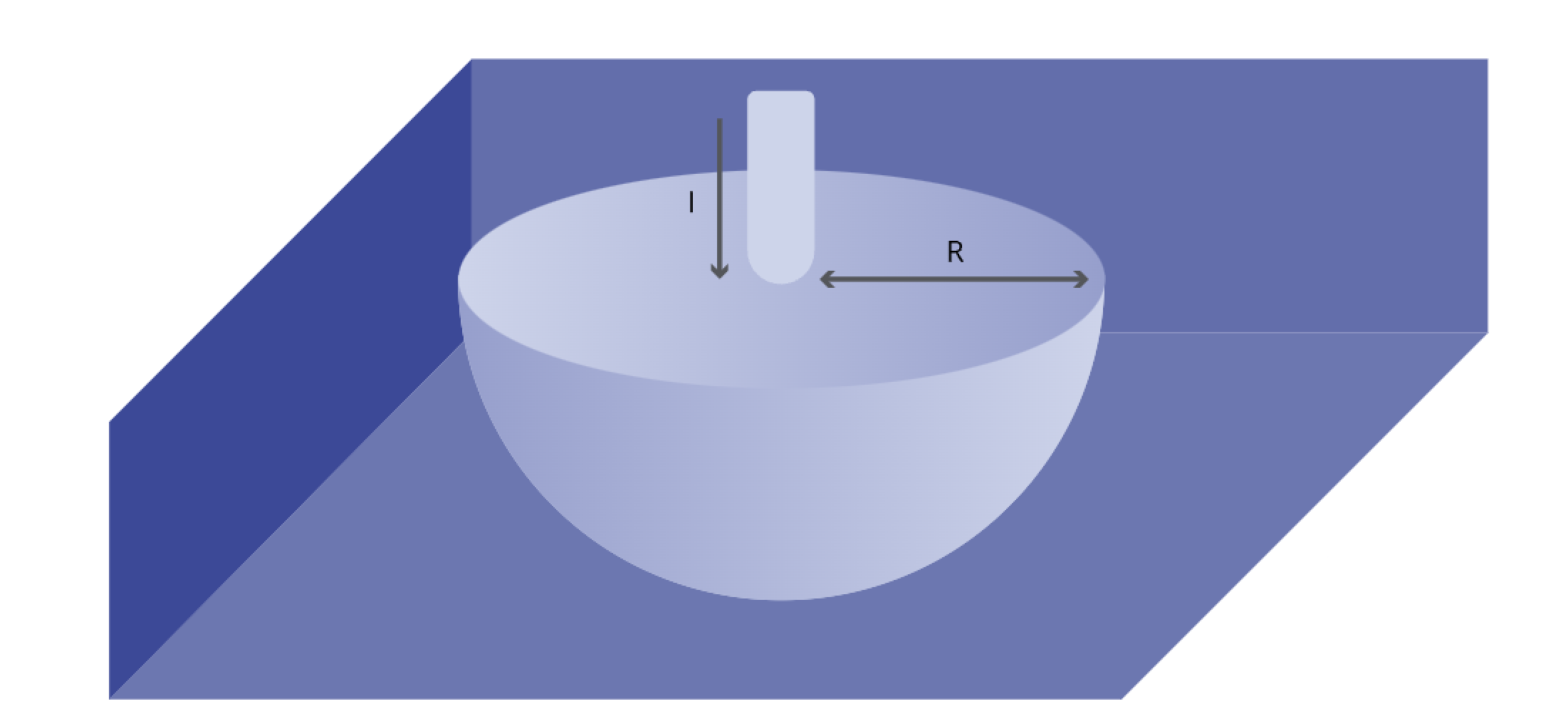
图1——技术咨询176-5252-0563

如图1，探针将电流I注入半无限体积的导电材料中。浅蓝色半球是注入电流的壳，半径为r，电流从接触点向外流过同心半球形等势壳，每个壳的电流密度(J)为:

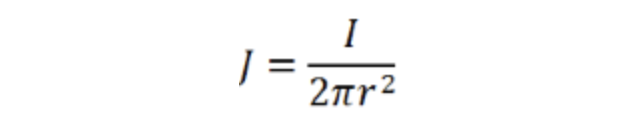
其中r是距探针的径向距离(2πr²是半球的表面积)。根据欧姆定律(E=pJ)，每个壳上的电场等于壳厚度上的电压差，或-V/Δr(该项为负，因为电压随r减小)，壳厚度趋于零，可得出以下方程:

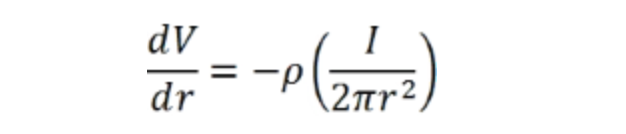
对r和r"进行积分以获得:

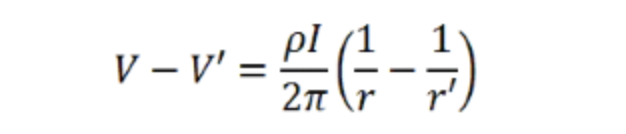
当r趋近于无穷大时，V将趋近于零，该方程简化为:

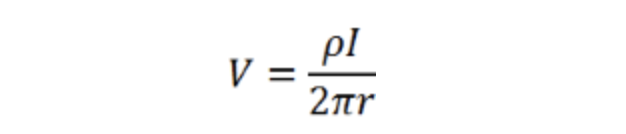
想象一下，有四个任意尖锐的探针(标记为1至4)与半无限导电材料接触，它们排成一线，间距相等(5)。它们的设置使得电流通过探针1注入并由探针4收集。如果假设每根探针具有等效边界条件，则任何一点的电压都等于每个探针单独产生的电压之和，即:

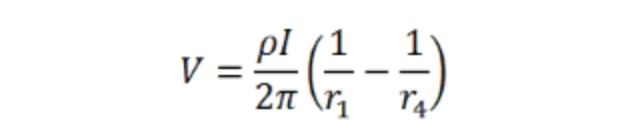
其中r1和r 4分别是探针1和探针4的径向距离。然后测量探针2和3之间的电压。使用上述公式，探针2和3处的电压为:

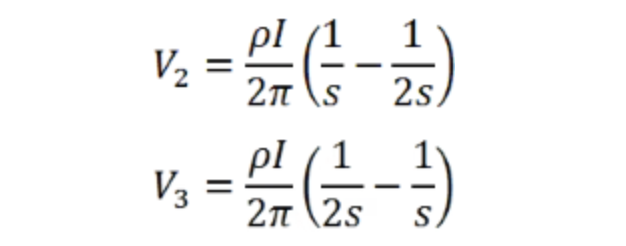
因此，探针2和3之间的电压变化(ΔV)为:

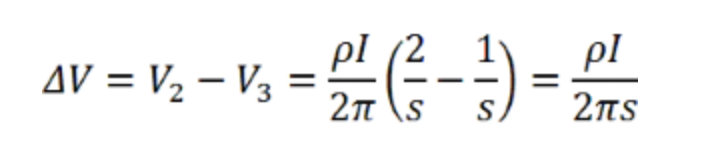
因此，探头之间的电阻率为:

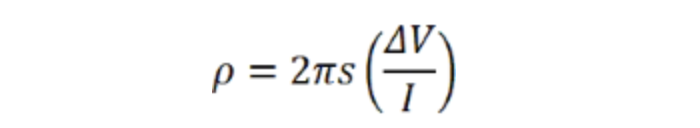
此表达式仅适用于半无限体积的情况，不适用于薄膜的情况。但是，可以使用类似的分析得出新的表达式。与之前一样，想象任意尖锐的探针接触厚度为t的材料薄膜并将电流注入其中。

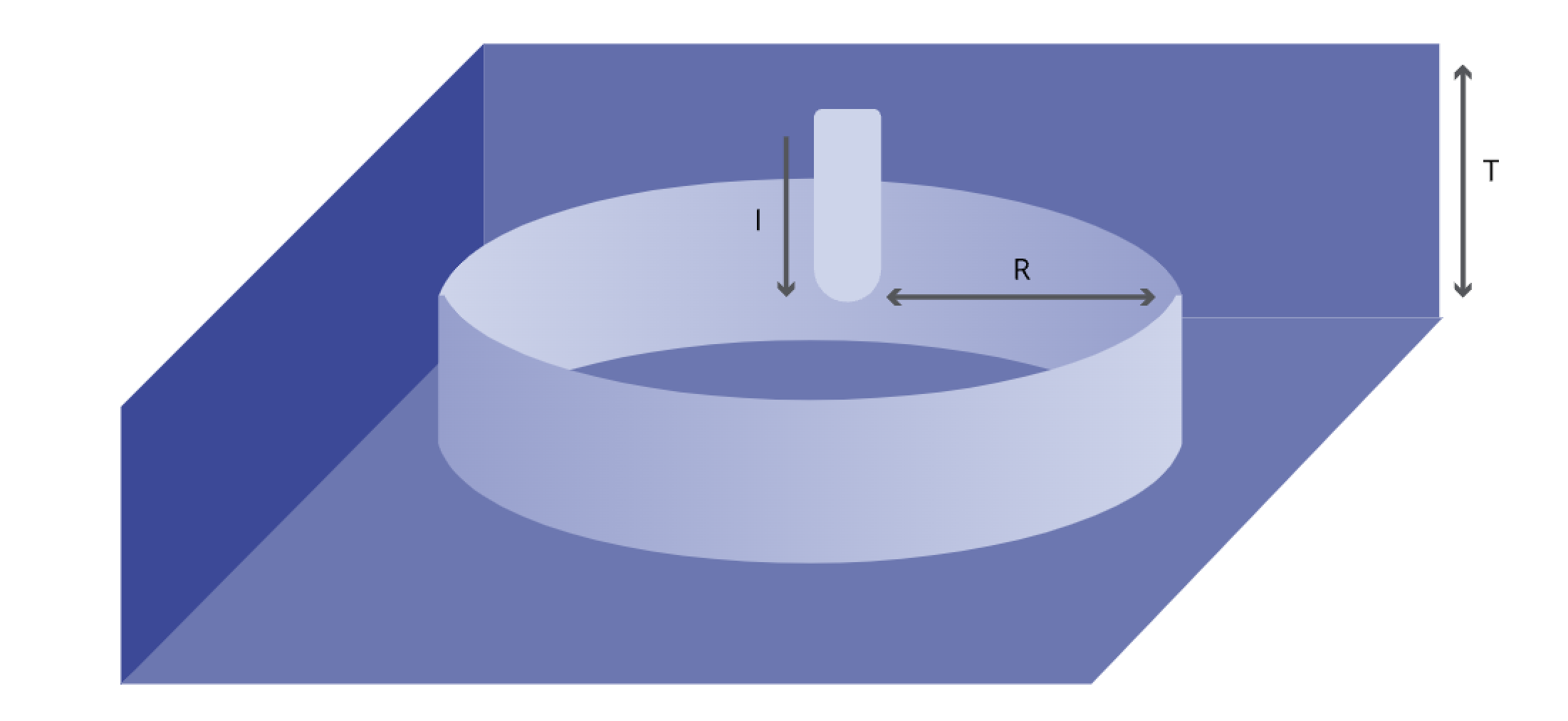
图2

如图2，探针将电流I注入厚度为t的导电材料薄膜，浅蓝色圆柱体是注入电流的壳体，半径为r。在这种情况下，电流从探头流出(通过材料)，流经等电位的短圆柱壳，每个圆柱壳的电流密度为:

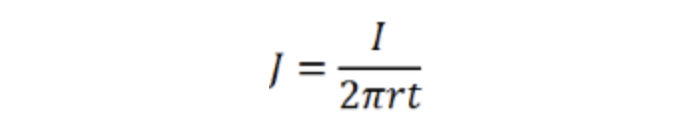
通过应用与之前相同的电场条件(欧姆定律和壳厚度趋于零)，每个壳上的电场为:

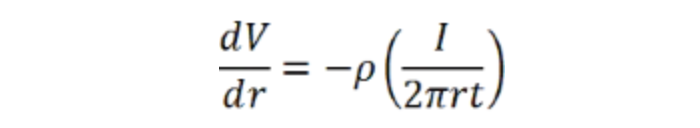
电阻率已定义为薄层电阻乘以材料厚度，因此可代入上式得出:

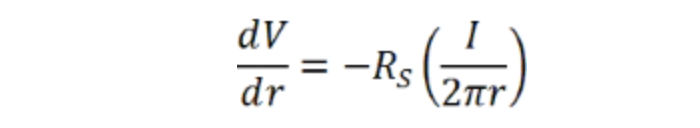
对r和r'进行积分以获得:

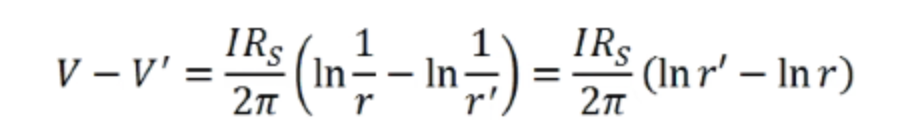
与之前不同，不能假设当r趋近于无穷大时电压会趋向于零，因为无穷大的自然对数不为零。然而，这并不影响分析，因为不同点的电压差(ΔV)是四探针测量的值。假设一下四探针系统与薄膜接触、并附加一个条件，即薄膜厚度(t)与探针间距(s)相比可以忽略不计。对于由探针1注入并由探针4收集的电流，方程变为:

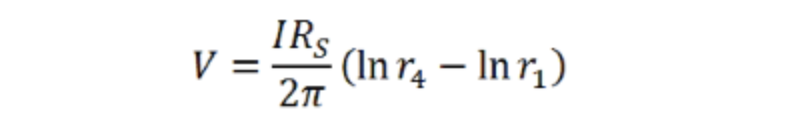
因此，在探针2和3处测得的电压为:

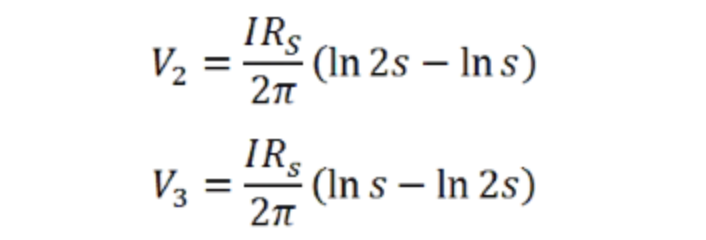
因此，电压的变化为:

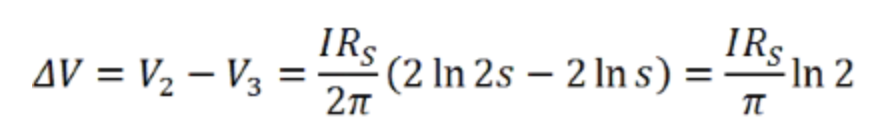
重新排列后可得：

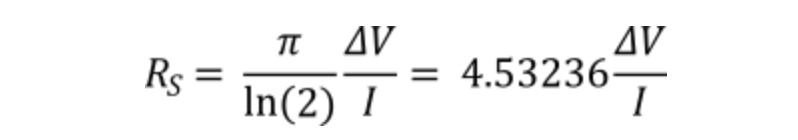
从上式可以看出，通过测量内探针之间的电压变化和外探针之间的施加电流，我们可以得到样品的薄层电阻。

丘山仪器全自动四探针电阻测试仪

丘山仪器四探针电阻测试仪的探针头借鉴了机械钟表机芯的制造工艺，使用红宝石轴承引导的碳化钨探针，以确保高机械精度和长使用寿命。其拥有1 μΩ~1 MΩ的超宽测量范围能涵盖绝大部分应用场景，可广泛适用于光伏、半导体、合金、陶瓷等诸多领域。