四探针原理｜薄层电阻校正因子

使用四点探针进行电气特性分析的主要优势之一是测量时无需考虑接触电阻和导线电阻。下图显示了四探针测量的电路电阻。

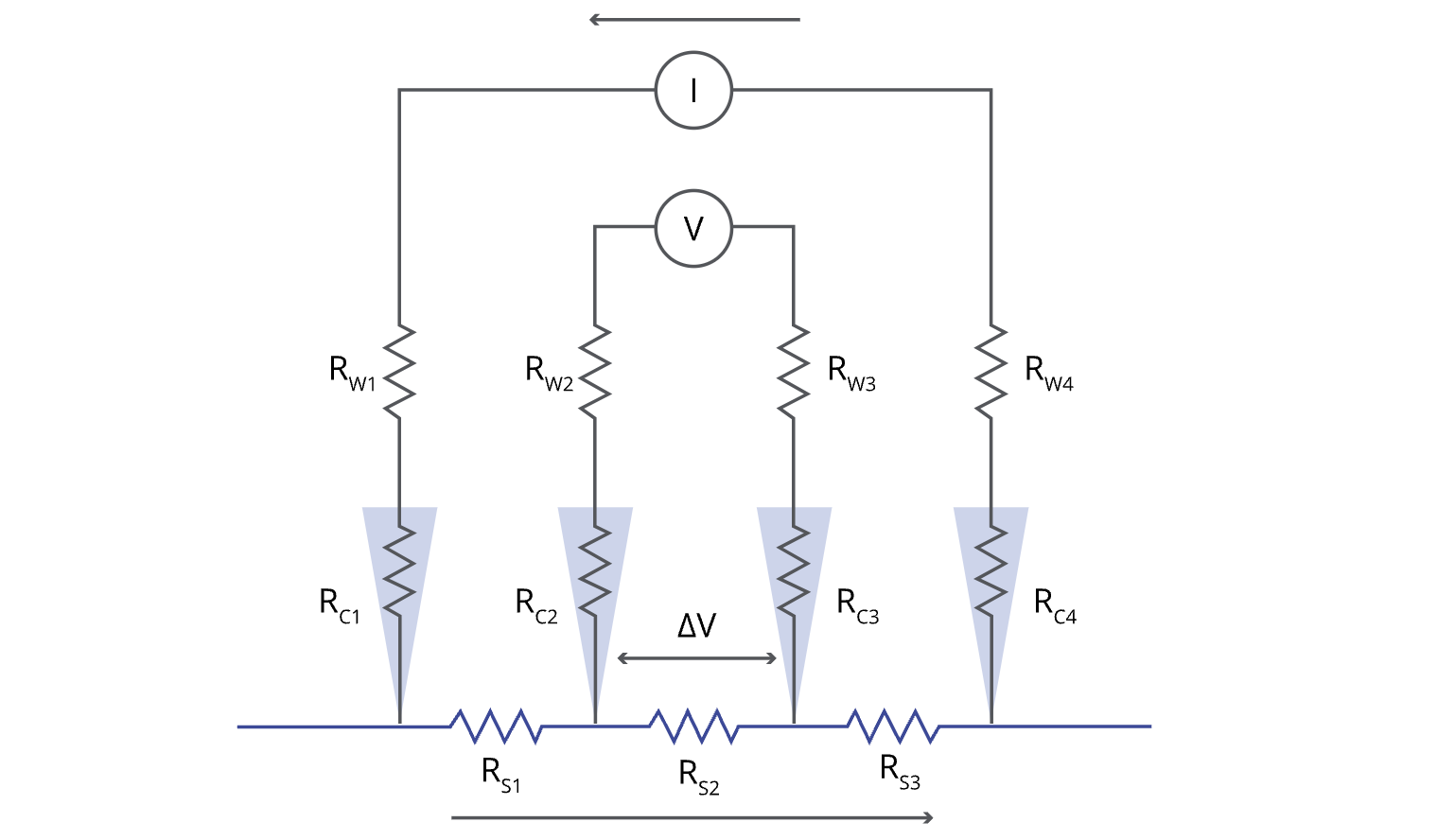
四探针的等效电路图——技术咨询176-5252-0563

图中导线电阻(Rw)、接触电阻(Rc)和样品电阻(Rs)，浅蓝色箭头表示电流流动，施加的电流I通过外部探针进入和离开样品，并流过样品。电压表通常具有高电阻抗，以防止其影响被测电路，因此没有电流流过内部两根探针。仅测量内部探针之间的电压，这意味着导线电阻(Rwz和Rw3)和接触电阻(Rc和Rc)对测量没有贡献。因此，任何测得的电压差(ΔV)都将完全来自样品电阻(Rs)。这简化了薄层电阻方程，因此只需要ΔV和施加的电流即可得到Rsz的值(即薄层电阻)。

虽然薄层电阻公式与样品几何形状无关，但只有当样品明显大于(通常尺寸大40 倍)探针间距，且样品厚度小于探针间距的 40% 时，该公式（Rs=πΔV/ In(2)I=4.53236ΔV/I）才适用。如果不是这种情况。探针之间的可能电流路径会受到样品边缘的接近度限制，从而导致薄层电阻估计过高。为了解释这种差异，需要根据样品的几何形状确定校正因子。

圆形样品：

对于直径为d的圆形样品，在样品中心测量，可使用以下公式计算校正系数:

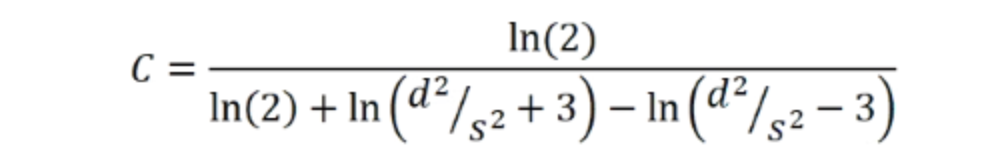
其中s是探针之间的距离。当d>>s时，该方程趋向于1，从而可以使用未修正的方程。

矩形样品：

对于矩形样品，几何校正因子的确定略微复杂，因此没有方程式，而是使用经验确定校正因子。表1中的值仅适用于探针接触样品中心并与样品最长边(1)平行的情况，如下所示。

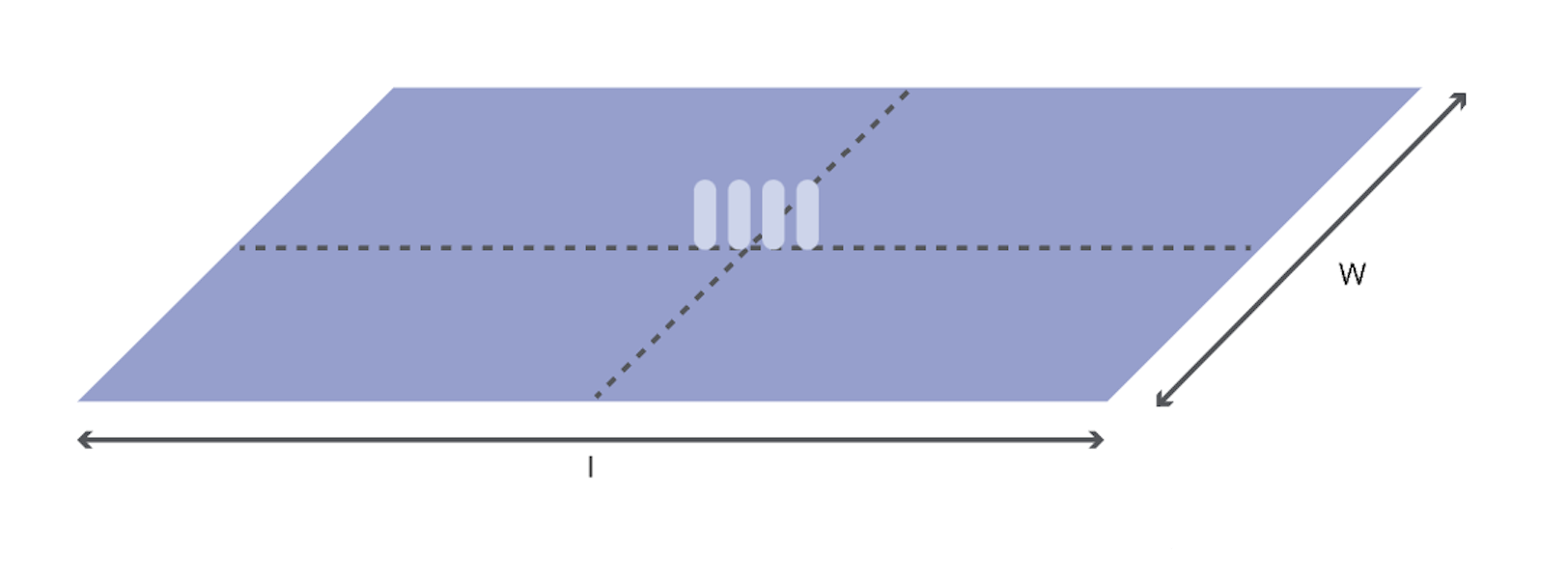
图中l≥w

举例来说，假设上图所示的矩形样品的长边为I=20mm，短边为w=10 mm，所用探针的间距为s=2mom，在这种情况下，I/w=2和w/s=5、因此在表中搜索满足这两个值的校正系数，沿l/w=2的列和w/s=5的行查找，即C=0.7887。将测量的薄层电阻乘以该值即可得到样品的正确值。

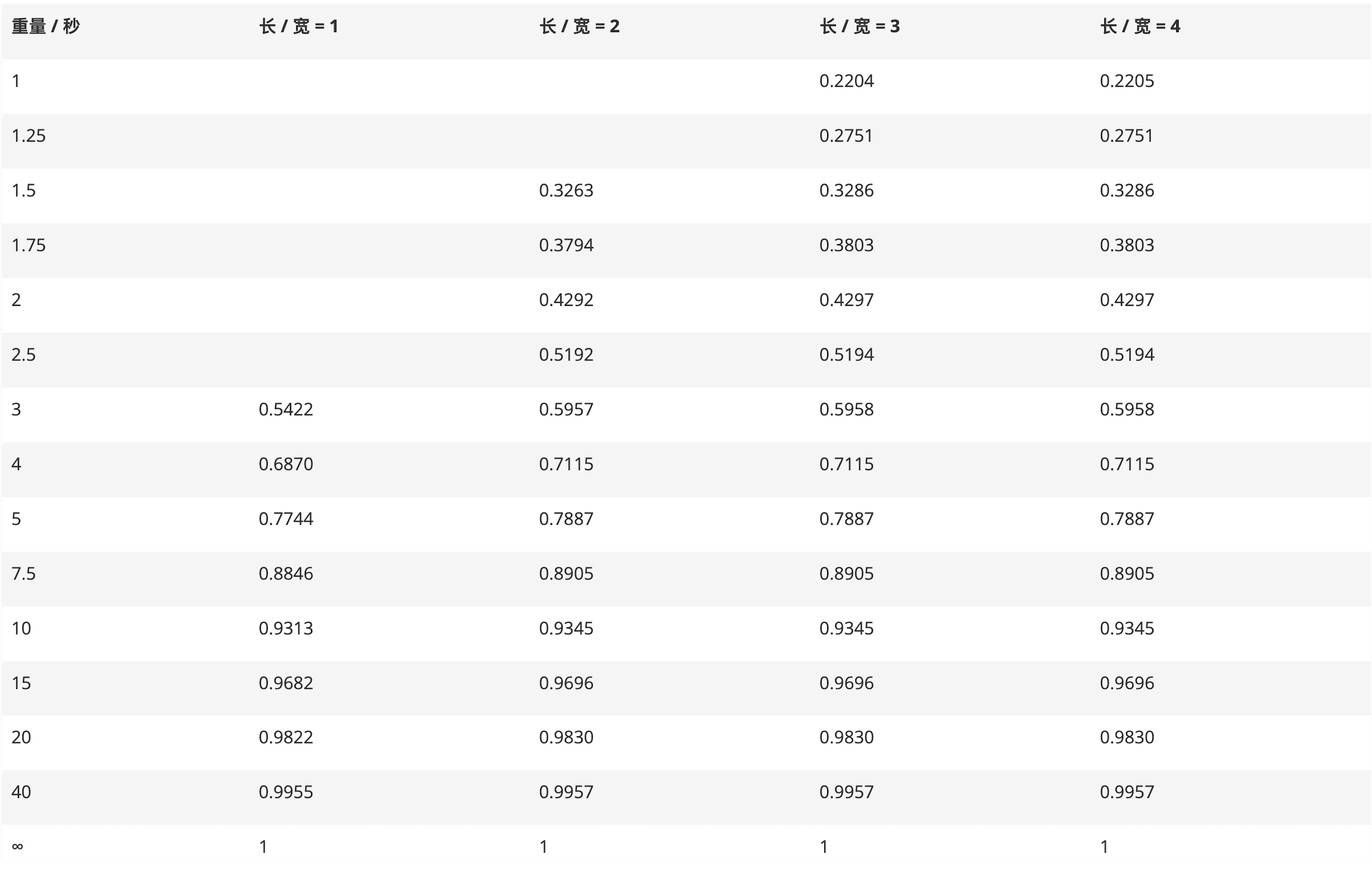
表1

并非所有样本都能恰好归入这些类别。如果是这种情况，建议使用三次样条插值来估计样本的适当校正系数。需要注意的是，上述圆形和矩形样品的校正系数仅适用于样品中心的测量。如果测量不在中心，则需要不同的校正系数。

如果被测样品的厚度大于探针间距的 40%，则需要额外的校正系数。所用的校正系数取决于样品厚度(t)与探针间距(s)的比率，下表2列出了一些可能的值。

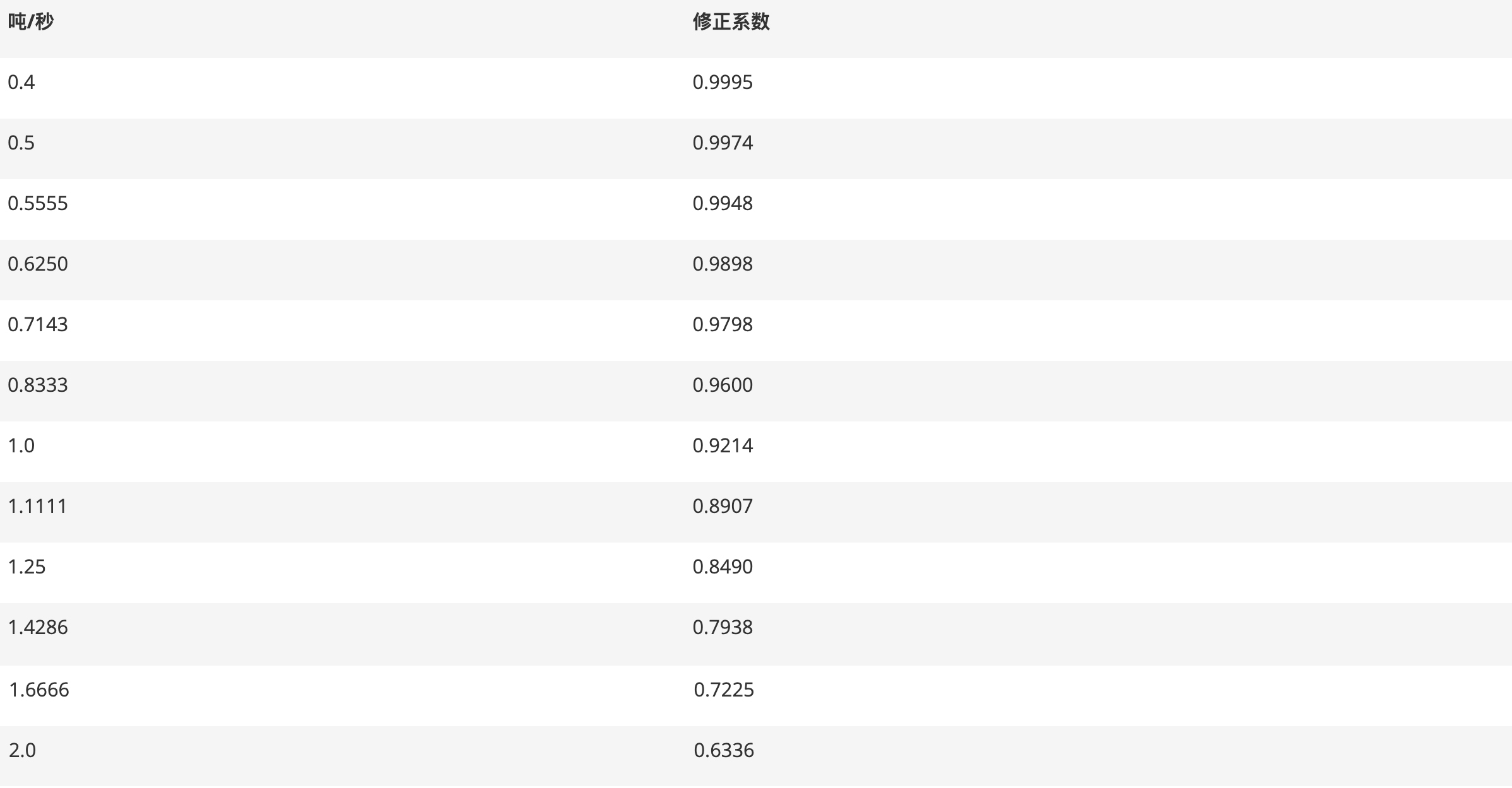
表2

与矩形样品一样，如果t/s不等于表中给出的值之一，则建议使用三次样条插值来估计样品的适当校正因子。

丘山仪器全自动四探针

丘山仪器四探针可以对最大 150mm 样品（或 6 英寸晶 圆）进行快速、自动的扫描，获得样品不同位置的方阻/电阻率分布信息，其动态测试重复性（接近真实场景）可达 0.2%，为行业领先水平，并且这款四探针电阻测试仪可广泛适用于光伏、半导体、合金、陶瓷等诸多领域。